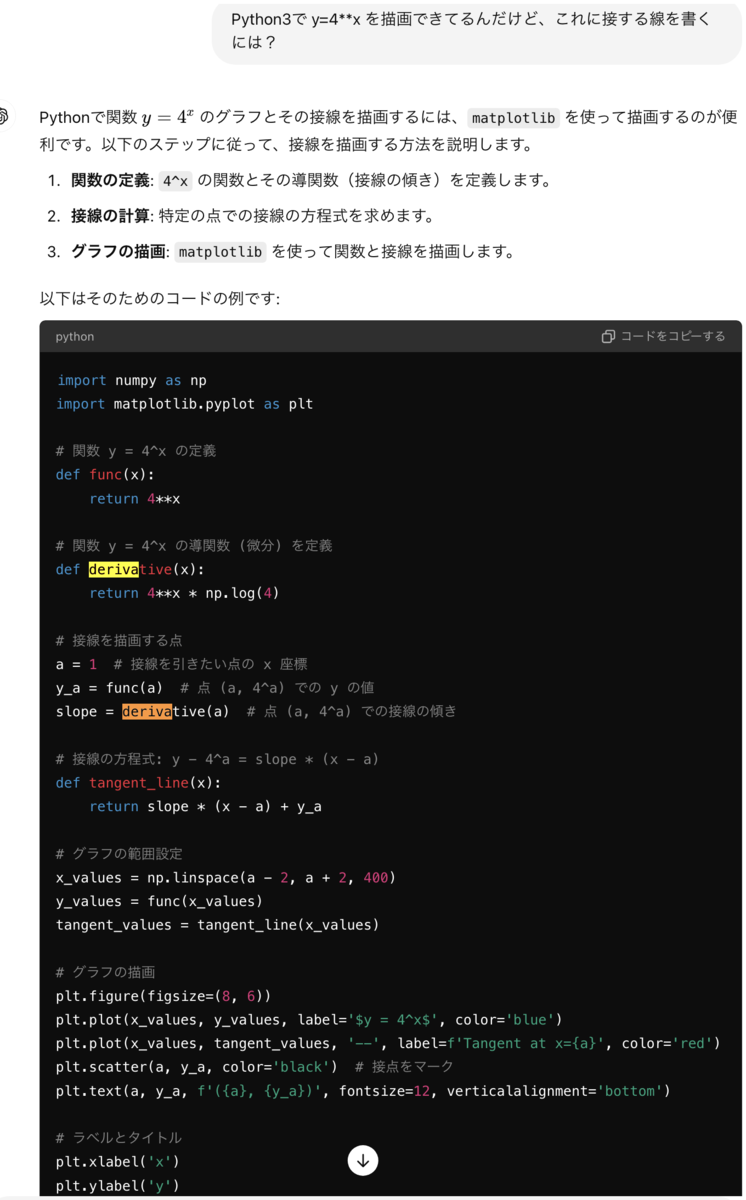
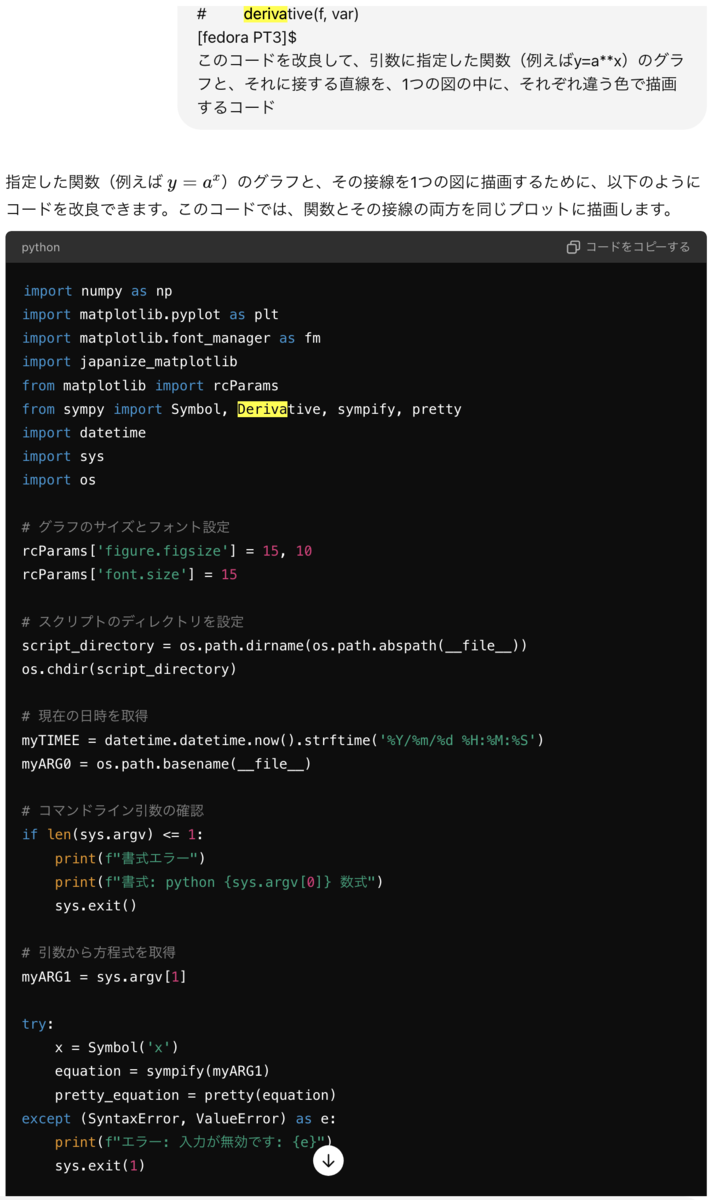
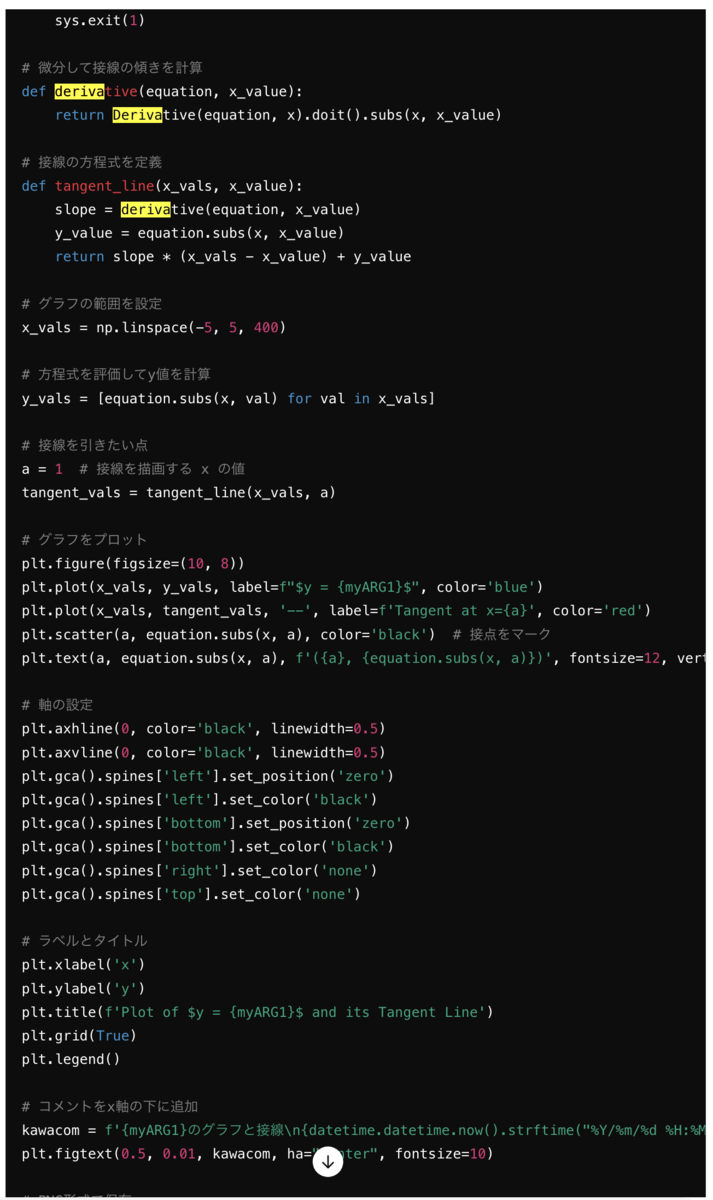
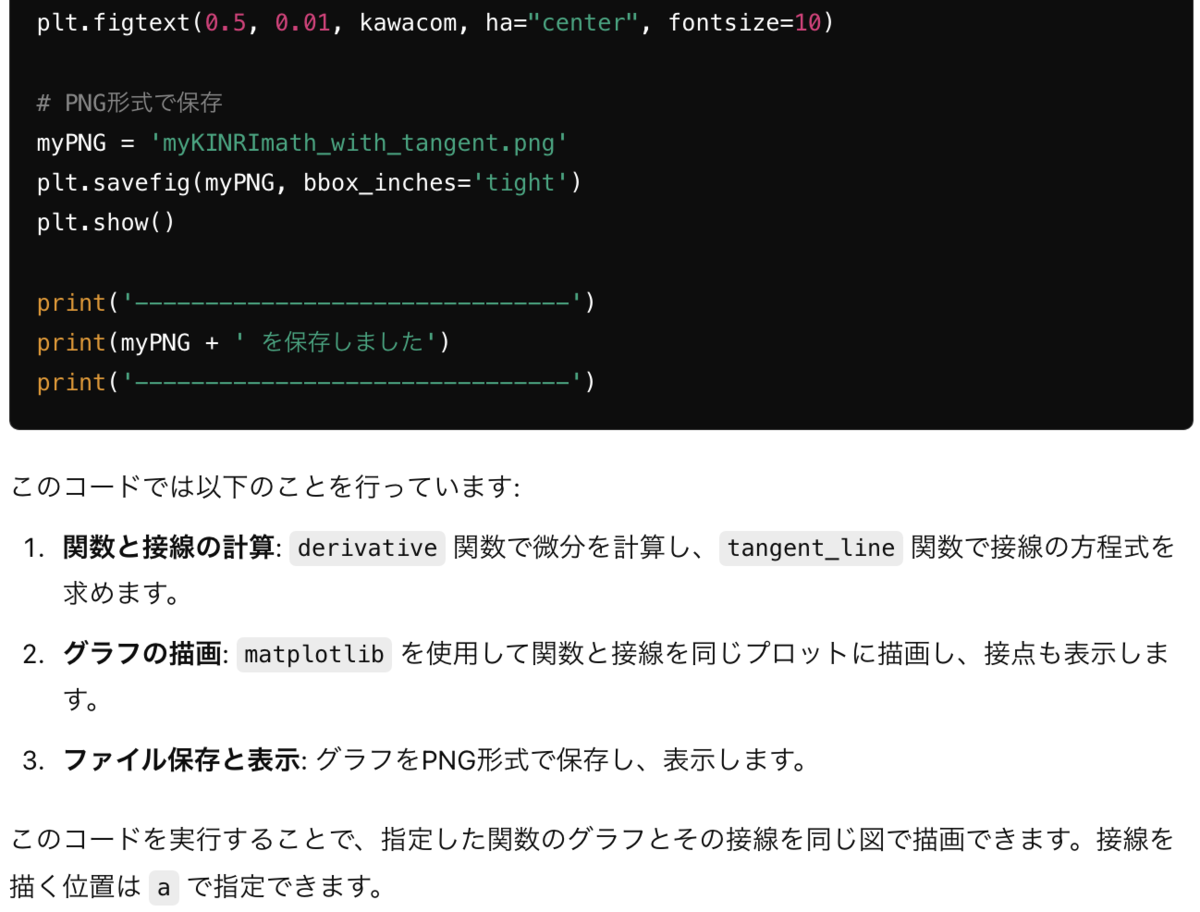
Pythonからはじめる数学入門で作った関数グラフで自然対数の底e（ネイピア数）を調べる

ネイピア数e をグラフで可視化したい

このyoutubeに出てきたグラフをPython3で描きたいのよ

www.youtube.com

できた

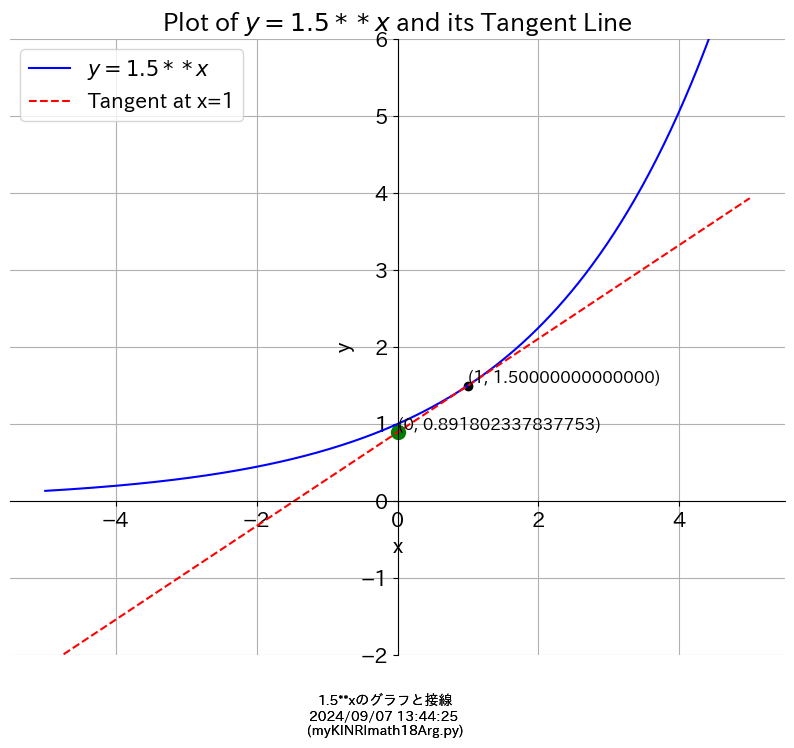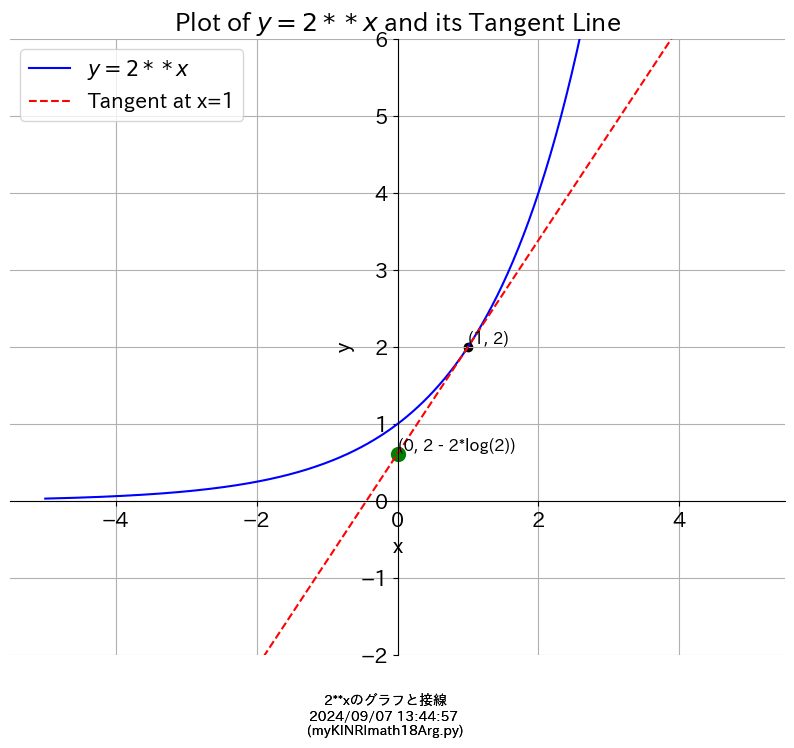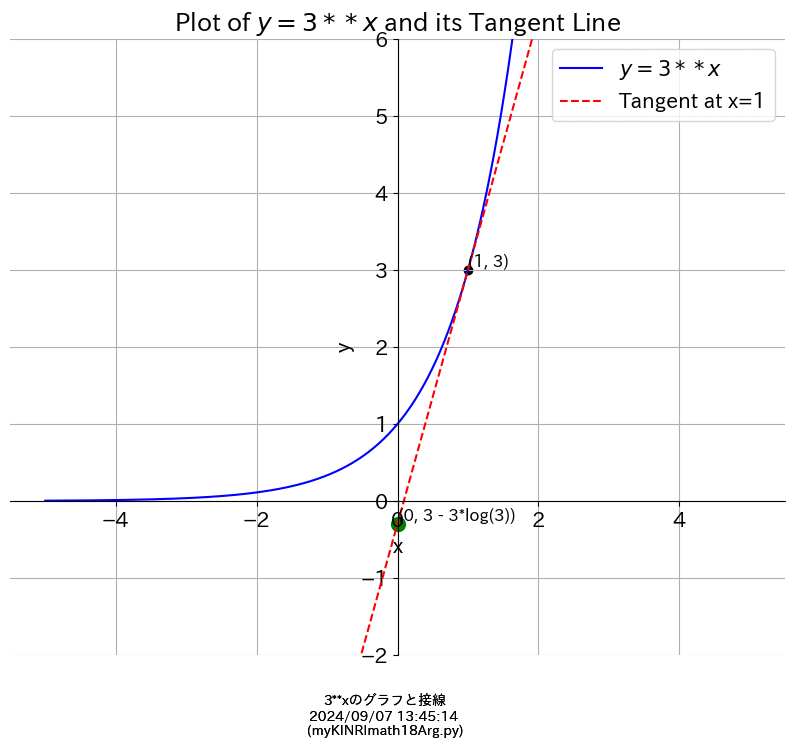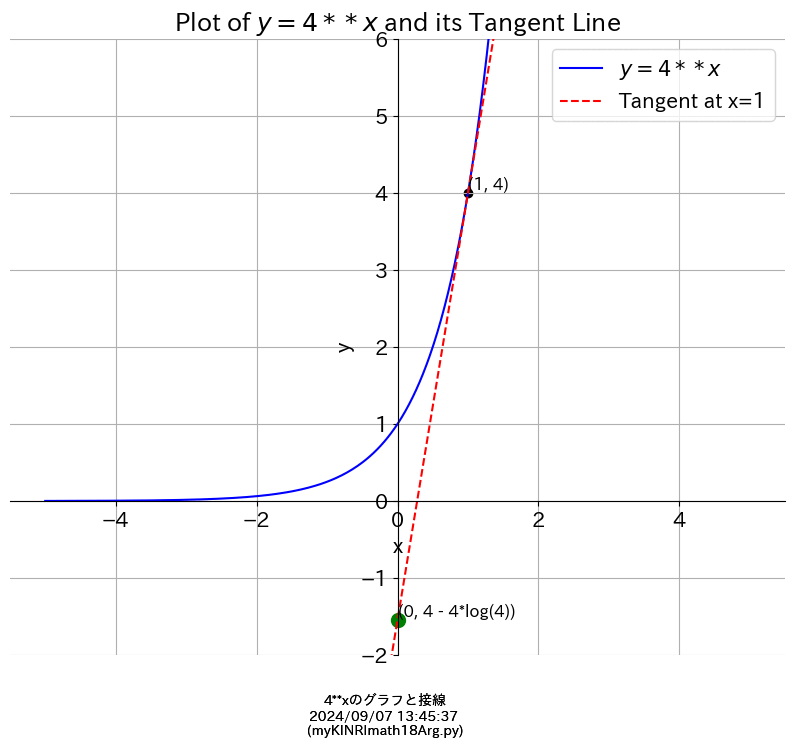
y = e**x（ネイピア数e）

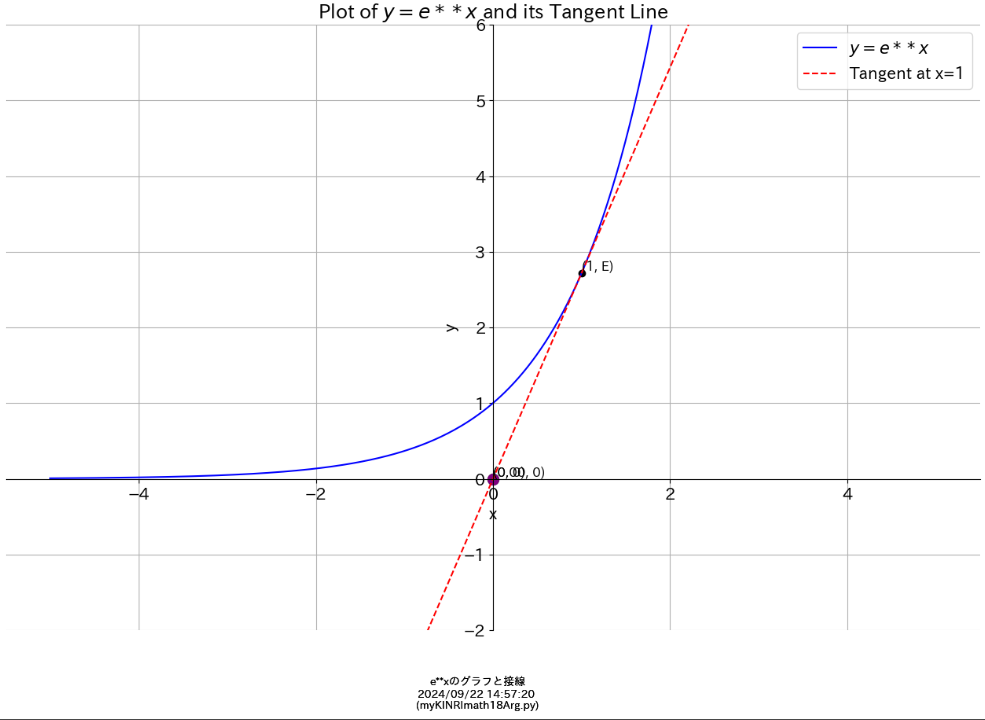
y = 2**x

（y＝2のx乗）とその接線 derivative（微分）

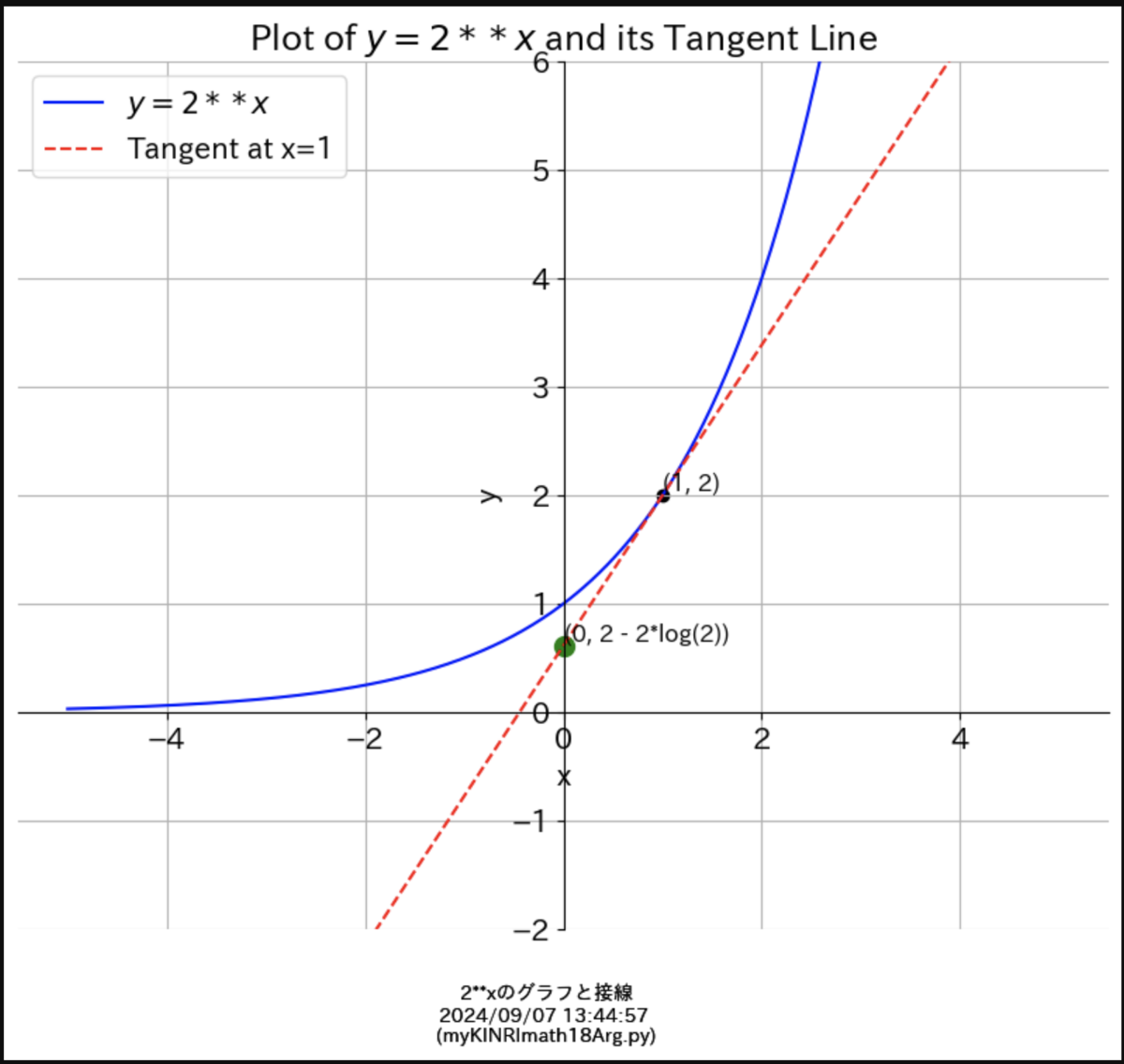
↑↓　ネイピア数はこの間にあるらしい

（↑↓それぞれの直線がy軸と接したところの間）

y = 3**x

（y＝3のx乗）とその接線 derivative（微分）

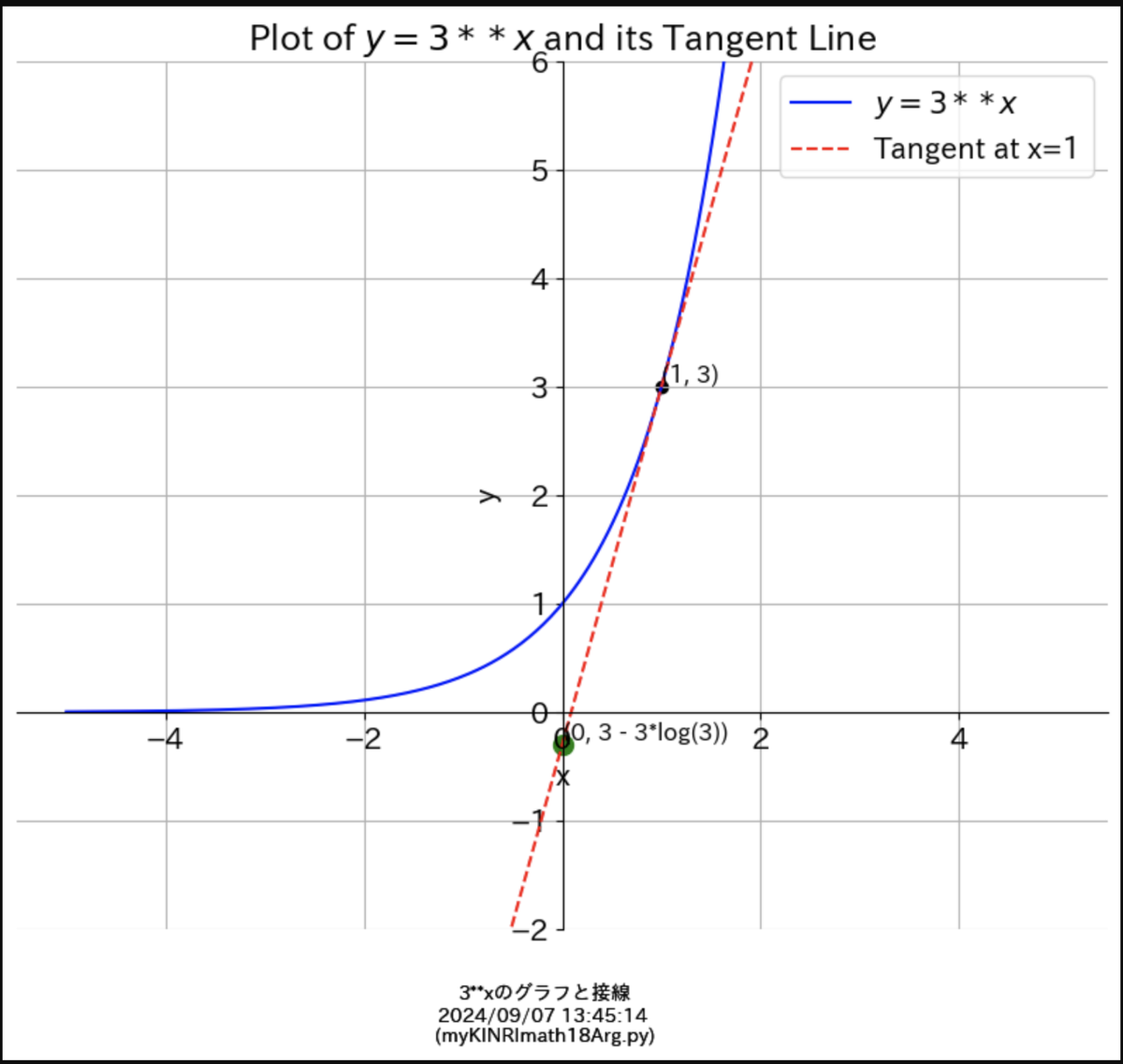
このあと

・y軸と接触したところに座標を表記したい

・2**x と 3**x とで縦軸（y軸）のメモリを合わせたい

↑

どっちもできた

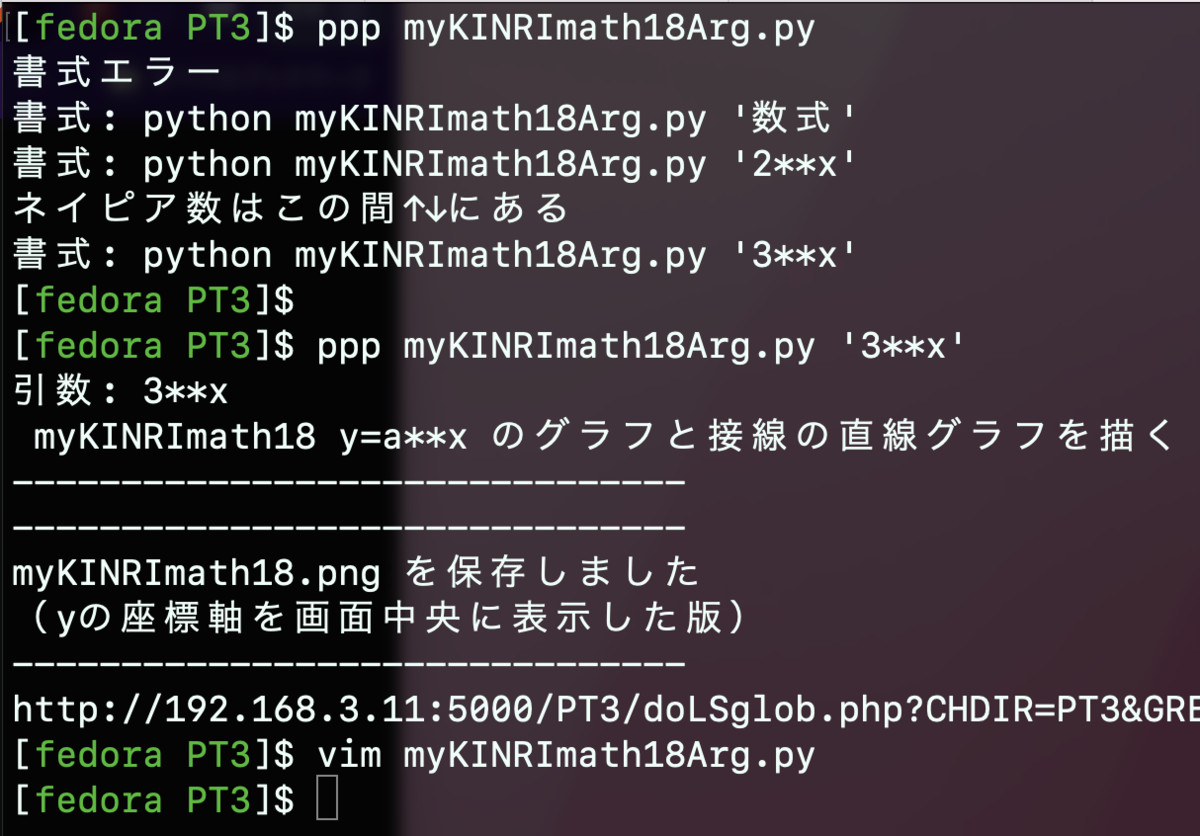
$ cat myKINRImath18Arg.py
import pandas as pd
import pandas_datareader as web

import matplotlib.pyplot as plt
# %matplotlib inline
import matplotlib.font_manager as fm
# plt.rcParams['font.family']='Droid Sans Japanese'
import japanize_matplotlib

from matplotlib import rcParams
rcParams['figure.figsize']=15,10
rcParams['font.size']=15
import sys
import os
import math

#import cv2
#from PIL import Image, ImageFont, ImageDraw
from PIL import Image
from PIL import ImageDraw
from PIL import ImageFont
import numpy as np

import subprocess

from sympy import Symbol, Derivative, sympify, pprint, pretty
from sympy.core.sympify import SympifyError
# ChatGPT from sympy import sympify, Symbol

import datetime
from datetime import datetime as dt
# import sys
# import os
# import numpy as np
# import matplotlib.pyplot as plt

import subprocess
# cdしないとcronで/rootに溜まっちゃう！
# スクリプトのディレクトリを取得
script_directory = os.path.dirname(os.path.abspath(__file__))

# スクリプトのディレクトリにカレントディレクトリを変更
os.chdir(script_directory)
#os.chdir('/media/WD30EZRX/PT3/')

# 現在の日時を取得
#execution_time = datetime.now().strftime("%Y-%m-%d %H:%M:%S")
myTIMEE = datetime.datetime.now().strftime('%Y/%m/%d %H:%M:%S')
myARG0 = os.path.basename(__file__)

if len(sys.argv) <= 1:
print(f"書式エラー")
print(f"書式: python {sys.argv[0]} \'数式\'")
print(f"書式: python {sys.argv[0]} \'2**x\'")
print('ネイピア数はこの間↑↓にある')
print(f"書式: python {sys.argv[0]} \'3**x\'")
sys.exit()

print(f"引数: {sys.argv[1]}")
#print(sys.argv[1])

myARG1 = sys.argv[1]

# print('Pythonからはじめる数学入門 20240901')
# print('-------------------------------')
# print('p203 高階微分と極大極小の計算で作ったコードを使って')
# print('-------------------------------')
# print('p120 入力した関数のグラフを描くコード')
# print('-------------------------------')

mySOURCE = (''' myKINRImath18 y=a**x のグラフと接線の直線グラフを描く''')

#mySOURCE = ('''
#ネイピア数　自然対数の底e とは\n
# https://www.youtube.com/watch?v=1M7FF1nd25I\n
#に出てきたグラフを描く''')
print(mySOURCE)
print('-------------------------------')

# ユーザーに方程式を入力させる
try:
#equation_input = input("プロットしたい方程式を入力してください（例: x**5 - 30*x**3 + 50*x）: ")
equation_input = myARG1
x = Symbol('x')
equation = sympify(equation_input)
#きれいな乗数表記をグラフのタイトルや吹き出しコメントで表示するために、SymPyのpretty関数やLaTeX形式を活用
pretty_equation = pretty(equation)
except (SyntaxError, ValueError) as e:
print(f"エラー: 入力が無効です: {e}")
sys.exit(1)

# 微分して接線の傾きを計算
def derivative(equation, x_value):
return Derivative(equation, x).doit().subs(x, x_value)

# 接線の方程式を定義
def tangent_line(x_vals, x_value):
slope = derivative(equation, x_value)
y_value = equation.subs(x, x_value)
return slope * (x_vals - x_value) + y_value

## xの範囲を設定
## x = np.linspace(-5, 5, 400)
## x = np.linspace(-10, 10, 400)
x_vals = np.linspace(-5, 5, 400)

## 方程式を定義
## y = x**5 - 30*x**3 + 50*x
## y = 2*x + 3
# 方程式を評価してy値を計算
y_vals = [equation.subs(x, val) for val in x_vals]

# 接線を引きたい点
a = 1 # 接線を描画する x の値
tangent_vals = tangent_line(x_vals, a)

# グラフをプロット
# plt.figure(figsize=(8, 6))
plt.figure(figsize=(10, 8))

# plt.plot(x, y, label=r"$x^5 - 30x^3 + 50x$")
#plt.plot(x, y, label=r"$2x + 3$")
#plt.plot(x_vals, y_vals, label=f"${equation_input}$")
plt.plot(x_vals, y_vals, label=f"$y = {myARG1}$", color='blue')
plt.plot(x_vals, tangent_vals, '--', label=f'Tangent at x={a}', color='red')
plt.scatter(a, equation.subs(x, a), color='black') # 接点をマーク
plt.text(a, equation.subs(x, a), f'({a}, {equation.subs(x, a)})', fontsize=12, verticalalignment='bottom')

# y軸を中央に配置
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.gca().spines['left'].set_position('zero')
plt.gca().spines['left'].set_color('black')
plt.gca().spines['bottom'].set_position('zero')
plt.gca().spines['bottom'].set_color('black')

# 右と上の枠線を消す
plt.gca().spines['right'].set_color('none')
plt.gca().spines['top'].set_color('none')

plt.xlabel('x')
plt.ylabel('y')
#plt.title('Plot of $x^5 - 30x^3 + 50x$')
# plt.title('Plot of 2x + 3')
#plt.title(f'Plot of ${equation_input}$')
plt.title(f'Plot of $y = {myARG1}$ and its Tangent Line')
#plt.title(f'Plot of ${pretty_equation}$')
plt.grid(True)
plt.legend()

# コメントをx軸の下に追加
# plt.figtext(0.5, -0.1, f"Script: {myARG0} | Executed on: {execution_time}", ha="center", fontsize=10)
# plt.figtext(0.5, -0.1, f"Script: {myARG0} | Executed on: {myTIMEE}", ha="center", fontsize=10)
kawacom = ''
kawacom = f'{myARG1}のグラフと接線\n{datetime.datetime.now().strftime("%Y/%m/%d %H:%M:%S")} \n({myARG0})'
plt.figtext(0.5, 0.01, kawacom, ha="center", fontsize=10)

#kawacom = datetime.datetime.now().strftime('%Y/%m/%d %H:%M:%S') + ' \n(' + myARG0 + ')'
#@ kawacom = mySOURCE + '\n' + datetime.datetime.now().strftime('%Y/%m/%d %H:%M:%S') + ' \n(' + myARG0 + ')'

## plt.xlabel(kawacom)
# コメントをx軸の欄外に追加
# plt.figtext(0.5, -0.2, kawacom, ha="center", fontsize=10)
plt.figtext(0.5, 0.01, kawacom, ha="center", fontsize=10)

# 数式を吹き出しコメントとして表示
# plt.annotate(rf"${equation_input}$", xy=(0.5, 0.5), xytext=(0.5, 0.75),
# textcoords='axes fraction', ha='center', va='center',
# bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
# arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.5'))

#math12 # グラフをプロット
#math12 plt.figure(figsize=(8, 6))
#math12 plt.plot(x, y, label=r"$x^5 - 30x^3 + 50x$")
#math12 plt.xlabel('x')
#math12 plt.ylabel('y')
#math12 plt.title('Plot of $x^5 - 30x^3 + 50x$')
#math12 plt.grid(True)
#math12 plt.legend()

myPNG = 'myKINRImath18.png'
# PNG形式で保存
# plt.savefig('myKINRImath12.png')
# plt.savefig(myPNG)
plt.savefig(myPNG, bbox_inches='tight')
#plt.show()
print('-------------------------------')
print(myPNG + ' を保存しました')
print('（yの座標軸を画面中央に表示した版）')
print('-------------------------------')
print('http://192.168.3.11:5000/PT3/doLSglob.php?CHDIR=PT3&GREPWORD=myKINRI&MKSORT=goMKSORT')

# def derivative(f, var):
# var = Symbol(var)
# d = Derivative(f, var).doit()
# pprint(d)
#
# if __name__ == '__main__':
# print('Enter a function:')
# f = input('微分したい（高次元の）関数を入力せよ:\n 例 2*x**2 + 3*x + 1 \n')
# print('-------------------------------------')
# print('Enter the variable to differentiate with respect to: ')
# var = input('微分に使う変数を指定せよ(xとか) ：')
# print('-------------------------------------')
# try:
# f = sympify(f)
# except SympifyError:
# print('Invalid input 不正な入力です')
# else:
# derivative(f, var)
[fedora PT3]$